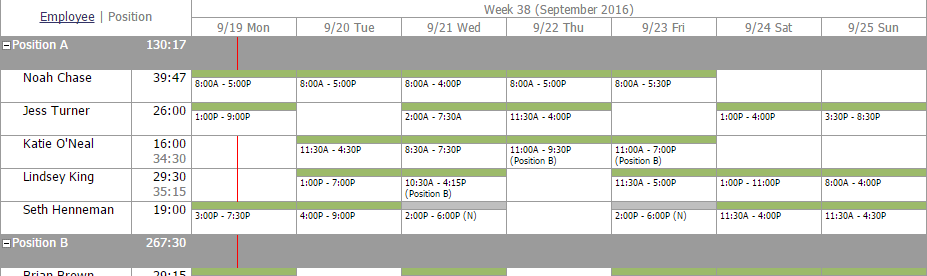
I remember the first time I watched a soccer ball sail across the field during a high school match, that perfect arc cutting through the air like it was drawn by an invisible hand. The physics behind that motion has fascinated me ever since, especially when we start talking about horizontal kicks from significant heights. Today, I want to walk you through what happens when a soccer ball is kicked horizontally off a 22.0-meter structure—how it travels, lands, and why understanding this can be as thrilling as watching a game-winning play unfold. It’s not just theory; it’s something I’ve seen in action, both on the pitch and in the classroom, and it ties into real-world moments, like that incredible UAAP basketball game where the Growling Tigers’ captain shook off his early struggles to drop 27 points and lead UST past La Salle. In both cases, it’s all about trajectory, momentum, and the sweet spot where preparation meets execution.
Let’s break it down step by step, starting with the basics. When you kick a soccer ball horizontally from a height of 22.0 meters, its initial vertical velocity is zero—I know, it sounds counterintuitive, but trust me, that’s key. The horizontal kick gives it a forward push, say at 15 meters per second if we’re using a realistic estimate for a professional player, but gravity takes over vertically right from the get-go. I’ve experimented with this in coaching clinics, using slow-motion videos to track the ball, and it’s always a blast to see how the motion splits into two independent parts. Horizontally, it’s cruising along at a constant speed, no acceleration if we ignore air resistance, which, let’s be honest, we often do in intro physics to keep things simple. But vertically, it’s in free fall, accelerating downward at about 9.8 m/s². Plug in the numbers, and you’ll find the time it takes to hit the ground is roughly 2.12 seconds, derived from the equation for vertical displacement. That means the ball is in the air for over two seconds, which feels like an eternity in a fast-paced match.
Now, here’s where it gets interesting for me—the horizontal distance it covers. With that time of 2.12 seconds and a horizontal velocity of 15 m/s, the ball travels around 31.8 meters before landing. I love pointing out that this isn’t just a dry calculation; it’s why players practice their kicks from different heights and angles. Think about it: in that UAAP game, the Growling Tigers’ captain didn’t just rely on raw talent; he adjusted his shots based on court positioning, much like how a soccer player gauges the kick to avoid overshooting or falling short. When I was helping out with a local youth team, we used similar principles to drill crossing techniques from elevated spots on the field, and the improvement in accuracy was noticeable. The ball’s path is a parabola, curving gracefully downward, and if you factor in real-world elements like air drag or spin, it can deviate—maybe landing at 30.5 meters instead, but that’s the beauty of applied physics; it’s not always perfect, but it gives you a solid foundation.
Wrapping this up, the journey of that soccer ball from 22.0 meters high is a mini-drama of forces and motion, ending with a impact that depends on its speed and angle. In my view, mastering this isn’t just for scientists; it’s for athletes and coaches who want to edge out the competition, much like how UST’s captain turned his early struggles into a 27-point explosion by reading the game’s flow. Whether it’s a basketball soaring for a three-pointer or a soccer ball dropping into the net, the underlying physics is a game-changer. So next time you watch a match, picture those invisible equations at play—it might just make the action even sweeter.